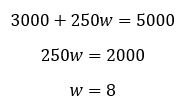When witches go riding and black cats are seen, the moon laughs and whispers, “’Tis near Halloween!” Whether you’re just starting your SAT prep or you’re getting ready for the November SAT, a little SAT math practice certainly never hurts. Since we’ve yet to figure out how to hand out candy through the Internet, we’re handing out Halloween SAT math practice problems instead.
Trick…or treat? You decide!
SAT Math Practice Questions
1. The frequency table above shows the results of a survey in which participants were asked how many lollipops they received while trick-or-treating. The median number of lollipops received by this group is
2. Glinda is selling candy bars for a fundraiser benefitting the Munchkins of Oz. If she wants to raise at least $400, and each bar she sells raises $1.25, which inequality can be used to determine whether selling c bars will meet Glinda’s goal?
3. A farmer plants apple trees and pumpkin vines. Each apple tree takes up 20 square feet of field, and each pumpkin vine takes up 16 square feet. If the farmer wants to use 1,968 square feet of field and plant 12 more apple trees than pumpkin vines, which system of equations should he use to determine how many apple trees he should plant? Assume a is the number of apple trees, and p is the number of pumpkin vines that the farmer plants.
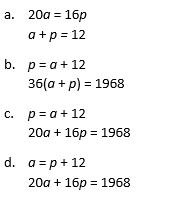
4. Dracula has two jobs, both of which have flexible hours. His job at a blood bank pays $15 per hour. His job polishing coffins pays $12 per hour. If he needs to earn $600 per week while working 44 hours per week, how many hours per week will he need to spend polishing coffins?
5. A mad scientist is measuring the growth of a sentient blob over time. The blob measures 300 square inches at the start of observation. It increases in size by 15% during the first week. It then decreases in size by 40% in the second week. What is its size after these changes?
6. A zombie horde’s goal is to increase its total size by 20% over two years, from 60,000 to 72,000 zombies. If an attack by zombie hunters results in a 20% decrease in the first year, by what percent must the zombie horde increase its size in the second year in order to meet its goal?
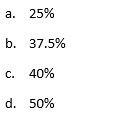
The next two questions use the following information.
The Halloweentown Candy Superstore conducts a poll of its customers to determine which types of candy are the most popular. Of the 300 responses, 30% picked chocolate bars, 25% picked jelly beans, 20% picked lollipops, and the rest picked another candy.
7. If the poll’s results are accurate and the candy store sells 1,207 pieces of candy on Halloween, approximately how many pieces of chocolate does it sell on Halloween?
8. As a follow-up question, the customers who chose a candy other than chocolate, jelly beans, and lollipops were asked to choose their favorite of those 3 candies. Two-thirds chose lollipops while the rest were evenly split between chocolate and jelly beans. What fraction of all customers prefers lollipops to chocolate and jelly beans?
9. A study of a local forest finds that the ideal ratio of werewolves to Sasquatches is 3:2. If there are currently 670 werewolves and 530 Sasquatches in the forest, how many werewolves must be added to the forest to reach the ideal ratio?
10. Victor Frankenstein earns $850 per week as a lab assistant. He has $3,000 in his bank account. He spends $600 per week and puts the rest of his earnings into his bank account. How many weeks will he have to work in order to have enough money in the bank to buy $5,000 worth of lab equipment for his secret science experiment?
The Answers
Below are the answers and explanations to the SAT math practice questions for you to review. How did you do?
1. The median number of a set of data will always be the middle data point when the data are arranged from least to greatest. If there are an even number of items in the data set, the median will be the mean of the two middlemost numbers. Since there are a total of
27 + 216 + 122 + 67 + 106 = 538 respondents, the two middlemost items in the data set must be the 269th and the 270th items. Both of these items correspond to respondents that received 2 lollipops, so the median of the data set is 2.
2. Since Glinda raises $1.25 for each candy bar she sells, and she sells c candy bars, we can determine the amount of money she raises by multiplying the amount per bar by the number of bars sold: $1.25c. The amount raised must be at least, or greater than or equal to, $400. So, the inequality that best represents this situation must be , which is shown in answer choice C.
3. Since each apple tree takes up 20 square feet, if the farmer plants a apple trees, he will need a total of 20a square feet of his field devoted to apple trees. Similarly, since each pumpkin vine takes up 16 square feet, he will need a total of 16p square feet of his field devoted to pumpkin vines. Sum these two areas and set them equal to the total area of field needed for the two plants: 20a + 16p = 1,968. We also know that the farmer wants to plant 12 more apple trees than pumpkin vines, we know that the equation a = 12 + p must also be true. These two equations are shown in answer choice D.
4. Let b be the number of hours Dracula spends working at the blood bank and c be the number of hours he spends polishing coffins. Since he wants to earn $600 per week, and we know he makes $15 per hour spent at the blood bank and $12 per hour spent polishing coffins, we can set up the equation 15b + 12c = 600. We also know he wants to work 44 hours, so we can write the equation b + c = 44. Solve the second equation for b, then plug it into the first equation and solve for c, the variable we’re asked to find:
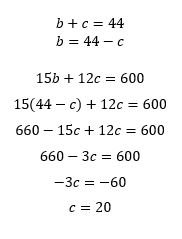
5. C. The first week, the blob increases its size by 15%. To calculate its new size, multiply the original size, 300 square inches, by 1.15 to get 345 square inches. Then, it decreases its size by 40%, so multiply this new size by 0.60 to get a final size of 207 square inches.
6. After the attack, the size of the horde is reduced from 60,000 to 60,000(0.80) = 48,000 zombies. Since the goal is to increase the size to 72,000, we must multiply the current size by what number to get there?
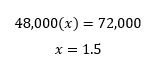
This indicates that the size must increase by 50% to make it to 72,000.
7. Since the poll results are accurate and are a large sample size relative to the total population of candy, set up a proportion:
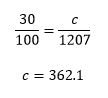
This is closest to answer C, 360 pieces of chocolate.
8. B. Since 30% of the original sample picked chocolate, 25% picked jelly beans, and 20% picked lollipops, the remaining 25% of the sample picked “Other”. Of these, two-thirds picked lollipops. So, the total portion of the sample who picked lollipops can be calculated by summing the portion who originally picked lollipops
and the fraction of those who picked other
which is the same as
This sum is 
9. 125. Currently, the ratio of werewolves to Sasquatches is 
but we want to add enough werewolves, w, to make this ratio equal to 
So, let’s solve for w by adding this variable to the current ratio and setting this equal to the ideal ratio:
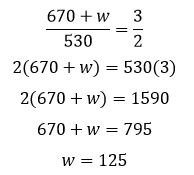
We need to add 125 more werewolves to the forest to reach the ideal ratio.
10. 8. Let’s set up an equation to represent the scenario, where w is the number of weeks that Victor works. He currently has $3,000. Every week, he gains $850 and spends $600, which leaves him with $250 a week to add to his savings. So, after w weeks, he can add 250w to his savings. Sum this with his current savings to see how many weeks it’ll take him to reach $5000:
