We know you’ve got a lot to be grateful for, but we want to add one more thing: Thanksgiving SAT math practice problems!
1- My grandmother used two coupons when purchasing the Thanksgiving ham. The first took $5 off her purchase. The second took an additional 25% off the reduced price. The final total was $12. What was the original price of the ham?
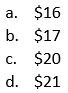
2- Two runners are participating in the annual Turkey Trot. Leroy runs at a constant rate of 6 miles per hour, and Kevin runs at a constant rate of 5 miles per hour. If Kevin has already run for 24 minutes by the time Leroy starts running the race, how far will Leroy have run when he catches up to Kevin?

3- For $20, a customer could purchase 2 pumpkin pies and 6 cans of cranberry sauce. At the same store, a customer could purchase 3 pumpkin pies and 4 cans of cranberry sauce for $5 more. How much more expensive is 1 pumpkin pie compared to 3 cans of cranberry sauce?
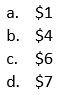
4- I volunteer at a soup kitchen every Thanksgiving. Last year, we used 248 carrots and 132 potatoes. This year, we will increase the number of carrots used by 50%. If we will use twice as many total carrots and potatoes this year as we did last year, how many potatoes will we use this year?
Questions 5 and 6 refer to the information below.
The circle below represents the family’s apple pie. The shaded area shows the slice that gluttonous Uncle Hobart took for himself after dinner. Major arc AB below has a length of 16.5 inches, while minor arc AB has a length of 11 inches.
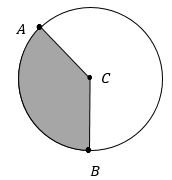
5- What is the measure of the central angle that forms Uncle Hobart’s slice of pie (minor arc AB)?

6- What is the diameter of the pie dish used to make the apple pie, rounded to the nearest inch?
![]()
Questions 7 and 8 refer to the information below.
| Age Group | Apple Pie | Pumpkin Pie | Cherry Pie | Pecan Pie | Total |
| 18-29 | 22 | 12 | 5 | 8 | 47 |
| 30-44 | 16 | 26 | 6 | 8 | 56 |
| 45-59 | 25 | 37 | 8 | 8 | 78 |
| 60+ | 31 | 23 | 7 | 8 | 69 |
| Total | 94 | 98 | 26 | 32 | 250 |
Two hundred and fifty members of the Pie-Lovers United Club were selected at random and asked to choose their favorite pie among four choices. The results of the survey are shown above and should be considered representative of the preferences of all 4000 members of the club.
7- What percentage of the members surveyed both prefer pumpkin pie and are between 18 and 29 years of age?
8- Based on the results of the survey, approximately how many members of the entire club prefer cherry pie?

9- Aunt Ginny’s secret stuffing recipe features 3 types of bread cubes: rye, cornbread, and Italian bread. I noticed that she used a total of 8 cups of bread cubes, of which 3 cups were rye bread cubes. She told me that she uses a 1 to 2 ratio of cornbread cubes to Italian bread cubes. How many cups of Italian bread cubes did she use?
10- My mother wants to serve both turkey and ham for Thanksgiving dinner. Turkeys are on sale for $1.00 per pound, and hams are on sale for $2.25 per pound. My mother wants to purchase a total of 20 pounds of meat for the meal, and she wants to spend $35.00. How big of a ham can she purchase?
And now, the answers…
1- Let h be the original price of the ham. First, subtract $5 from that price for the first coupon to get the quantity (h – 5). Since her second coupon takes 25% off of this reduced price, we can calculate the price after the coupon by multiplying this quantity by ![]() Now we can set up an equation and solve:
Now we can set up an equation and solve:
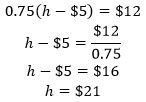
2- D. Since Kevin runs for 24 minutes ![]() more than Leroy does, we know that if Leroy runs for t hours, then Kevin will run for (t + 0.4) hours. We also know that the two runners run the same distance, d, and that distance equals the product of the runner’s rate and his time spent running. Since we know that d = r x t, we can use all of this to solve:
more than Leroy does, we know that if Leroy runs for t hours, then Kevin will run for (t + 0.4) hours. We also know that the two runners run the same distance, d, and that distance equals the product of the runner’s rate and his time spent running. Since we know that d = r x t, we can use all of this to solve:
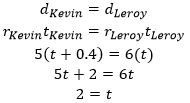
So, we know that Leroy runs for hours before he catches up to Kevin. Thus, Leroy’s distance traveled to catch up to Kevin is:
![]()
3- B. Set up a system of equations (with p equal to the number of pumpkin pies and c equal to the number of cans of cranberry sauce), with one representing the price of the first set of purchases and the other representing the second set of purchases:
![]()
Then, use the elimination strategy for solving system of equations. Multiply the top equation by -3, the bottom equation by 2, and then add the equations together to get:
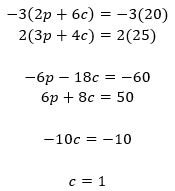
So, a can of cranberry sauce costs $1. Plug this into the first equation to find the cost of a pie:
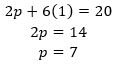
So, 1 pumpkin pie costs $7, while 3 cans of cranberry sauce cost 3(1) = $3. The difference is $7 – $3 = $4.
4- After increasing the number of carrots by 50%, we will have 248(1.5) = 372. Overall, the total number of carrots and potatoes used is twice as much as last year, or equal to 2(248 + 132) = 760. Subtract from this new total number of vegetables the new number of carrots, 372, to get 760 – 372 = 388 potatoes.
5- The ratio between the arc length and the circumference of a circle is always equivalent to the ratio of the measure of the central angle to 360 degrees:
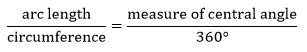
Since we know the length of the minor arc and major arc, add these together to find the length of the circumference, 27.5 inches. Plug in the values we know and solve:
 6- D. Since we already determined that the length of the circumference is 27.5 inches, use the formula
6- D. Since we already determined that the length of the circumference is 27.5 inches, use the formula ![]() to find the approximate length of the diameter of the dish:
to find the approximate length of the diameter of the dish:
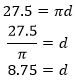
So, the length of the diameter is approximately 9 inches.
7- A. Looking at the table, we see that only 12 members from the sample group both prefer pumpkin pie and are in the 18-29 year old age group. Divide this number by the total number of people sampled, 250, to get ![]() of the surveyed members.
of the surveyed members.
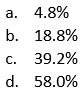
8- D. Since the survey is considered representative of the overall club, we know the percentage of people in the survey who prefer cherry pie should be approximately the same as the percentage of people in the overall club who prefer cherry pie:
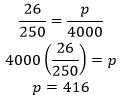
9- 10/3 cups. Since 3 of the cups of bread are rye, the remaining 8 – 3 = 5 cups must be a combination of cornbread and Italian bread. Since the ratio of cornbread to Italian bread is 1 to 2, we know that the ratio of
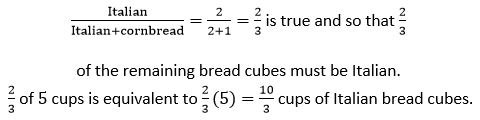
10- 12 pounds. Let h be the number of pounds of ham used and t be the number of pounds of turkey. We know the two equations below must be valid, one for the weight of meat and one for the price of meat:
![]()
Solve the bottom equation for and plug it into the top equation, then solve for h:
![]()
So,
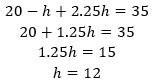
So, my mother can buy a ham that is 12 pounds.
Did you enjoy these mathematics practice problems? Start SAT prep with C2 today!









